Metric Noise Resource (MNR)

Motivation

The Metric-Noise-Resource (MNR) methodology was introduced in 2022 by M. Fellous-Asiani et al. [1] in the context of the Quantum Energy Initiative [2]. The authors motivate the creation of this methodology by the need for a multi-level approach to understand and optimize the resource consumption of quantum computers. As explained by the authors, such an approach requires a strong knowledge of quantum processors at a physical level (e.g., quantum control) and at a software level (e.g., quantum error correction and quantum algorithms). This methodology aims to obtain a clear view of how resources will scale with the size of the computational task.

Methodology

The MNR methodology aims to minimize the resources \(\mathcal{R}\) required by a quantum computer to reach a specific target metric \(\mathcal{M}\) and to identify/analyse non-trivial trade-offs between the parameters under study. This minimization is done with respect to the determined control parameters.

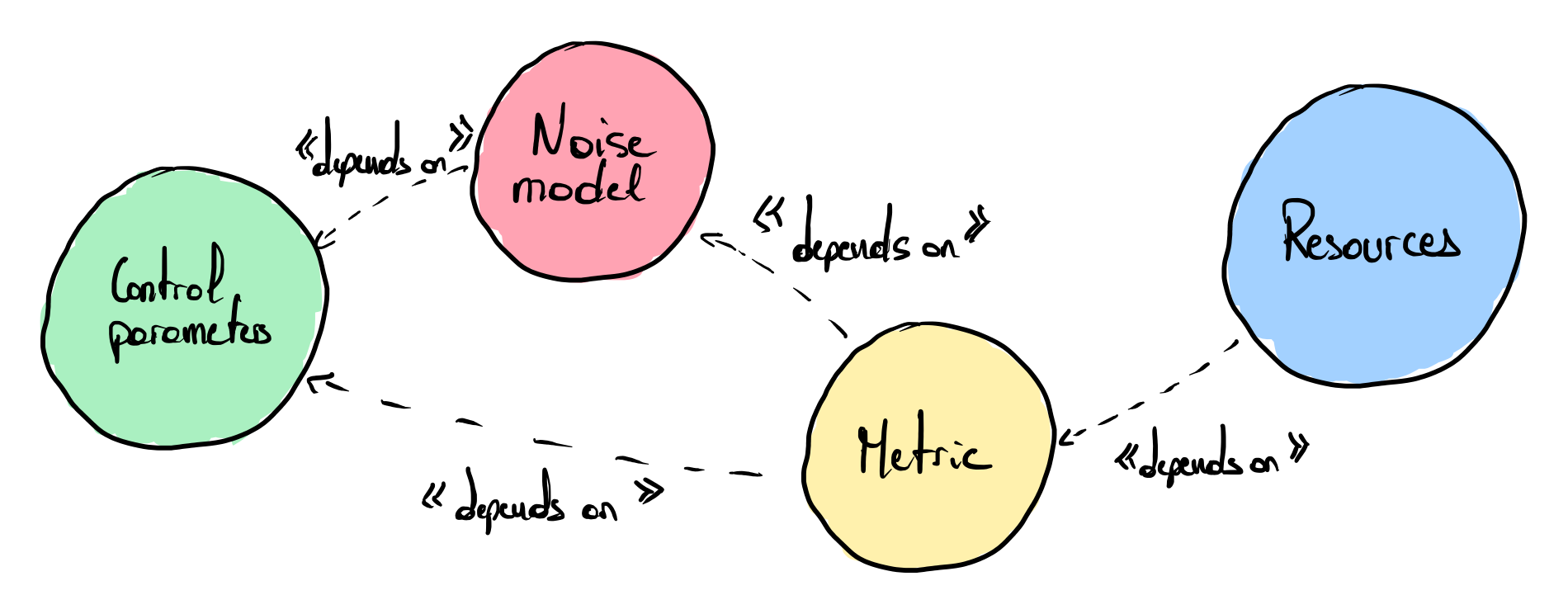
The MNR methodology comprises several components (see figure for the dependency between the main components):

• Control parameters: The parameters can span the physical level (such as the operating temperature of the qubits) and the software-level (as the size of the quantum error correction code or any quantity qualifying the architecture of the quantum computer).
• Performance metric: The metric \(\mathcal{M}\) evaluates the quality of the output of the quantum computer. The metric is set to a fixed satisfying target value \(\mathcal{M}_0\), which permits optimizing the control parameters.
• Noise model: The noise model defines how the noise impacts the system’s evolution. The noise model is closely linked to the control parameters’ settings and directly impacts the performance metric.
• Resources: It defines the resources of interest, whose consumption has to be minimized. The resources can take different shapes at different levels of the quantum software stack (e.g., it can be the time required to run a quantum algorithm, the energy consumption, the physical volume occupied by a quantum processor, etc.).

The resource efficiency \(\eta = \mathcal{M} / \mathcal{R}\) is a ratio between the metric \(\mathcal{M}\) and the resources \(\mathcal{R}\) (inspired by the Flops/Watt efficiency metric used in the Green500 ranking). The MNR methodology aims to minimize the resources \(\mathcal{R}\) required to reach a specific target metric \(\mathcal{M}\).

Implementation Examples

Different examples using this methodology are given in the initial paper [1]. These examples use simplified models to provide insights about resource consumption scaling.

Noisy single-qubit gate implementation (quantum-level)

Section III. A of [1] minimizes the power consumption of quantum gates to reach a satisfying fidelity. It studies the trade-offs between:

• The duration of a quantum gate, which is directly linked to its power consumption. Indeed, as the duration gets shorter, the required power increases.
• The error rate of the quantum gate (in particular, the probability of getting a spontaneous emission). The error rate increases with the duration of the quantum gate.

The following parameters are considered:

• Control parameters: Duration of the microwave pulse.
• Performance metric: Worst-case infidelity of the quantum gate.
• Noise model: The action of the noise is described by an equation depending on the duration of the microwave pulse.
• Resources: The power consumption of the quantum gate.

Noisy single-qubit gate implementation (macroscopic-level)

Section III. B of [1] minimizes the power consumption, including higher-level controls and the cryostat. It studies the trade-offs between:

• The temperature of the qubits in the cryostat and the attenuation factor that lowers the input pulse corresponding to the quantum gate.
• The power the cryogenic system requires to realize the quantum gate with a specific fidelity. The power consumption of the cryogenic system increases as the temperature of the qubits gets lower (as well as for higher attenuation factors), which reduces the errors.

The following parameters are considered:

• Control parameters: The attenuation factor of the attenuators in the control line, and the temperature of the qubits.
• Performance metric: Worst-case infidelity of the quantum gate.
• Noise model: The noise of the gate is described by an equation depending on both control parameters.
• Resources: The power consumption of the cryogenic system.

Circuit compression degree

Section IV of [1] studies the degree of compression of the quantum circuit and its impact on the power consumption of the quantum computer. It highlights the trade-offs between:

• The degree of compression of the circuit (ability to run quantum gates in parallel), the attenuation factor, and the temperature of the qubits.
• The total power required by the cryogenic system to run the circuit.

As the circuit gets compressed, its fidelity increases because qubits have only short idling times. However, running multiple gates at once increases the system’s power consumption.

The following parameters are considered:

• Control parameters: The attenuation factor of the attenuators in the control line, the temperature of the qubits, and the circuit compression factor.
• Performance metric: An approximation of the worst-case fidelity of the quantum circuit.
• Noise model: The noise of the gates is described by an equation depending on both the attenuation factor and the temperature of the qubits.
• Resources: The power consumption of the cryogenic system.

Fault-tolerant factorization

Section V of [1] studies the potential advantage of a quantum computer implementing Shor’s algorithm using the Steane code (a fault-tolerant quantum error correction code). It highlights the trade-offs between:

• The number of concatenation layers in the code (the fidelity of the quantum circuit increases with the number of layers).
• The power required to execute the fault-tolerant quantum circuit and the execution duration. The power consumption and duration of the algorithm increase with the number of layers.

Interestingly, the authors show that it is sometimes energetically more interesting to put qubits at a higher temperature and compensate with the quantum error correction code. They also show that in a specific regime, the quantum computer could factor RSA using more time than a classical computer, but consuming less energy.

The following parameters are considered:

• Control parameters: The temperature of the qubits, the temperature of the signal generation, the attenuation factor, and the number of layers in the quantum error correction code.
• Performance metric: The success probability of the quantum circuit (derived from the logical error rate).
• Noise model: The noise model is reduced to the physical error rate of the quantum gates.
• Resources: Power consumption of the system to run the quantum algorithm and execution time

References

1. [1]M. Fellous-Asiani, J. H. Chai, Y. Thonnart, H. K. Ng, R. S. Whitney, and A. Auffèves, “Optimizing Resource Efficiencies for Scalable Full-Stack Quantum Computers,” PRX Quantum, vol. 4, no. 4, Oct. 2023, doi: 10.1103/prxquantum.4.040319. [Online]. Available at: http://dx.doi.org/10.1103/PRXQuantum.4.040319
2. [2]A. Auffèves, “Quantum Technologies Need a Quantum Energy Initiative,” PRX Quantum, vol. 3, no. 2, Jun. 2022, doi: 10.1103/prxquantum.3.020101. [Online]. Available at: http://dx.doi.org/10.1103/PRXQuantum.3.020101